这是网上经常见的视觉错觉艺术图片，可以用程序生成的。效果如下：

完整的源代码如下：

///////////////////////////////////////////////////
// 程序名称：视觉错觉艺术4
// 编译环境：Visual C++ 6.0 / 2013，EasyX 20140321(beta)
// 作　　者：yangw80 <yw80@qq.com>
// 最后修改：2014-7-15
//
#include <graphics.h>
#include <conio.h>


// 定义回调
void (*callback)(int x, int y);


// 画方块上的小方块
void DrawSmallBox(int x, int y, bool lt, bool rt, bool lb, bool rb)
{
	int nx = x * 26 - 13;
	int ny = y * 26 - 13;
	if

这是网上经常见的视觉错觉艺术图片，可以用程序生成的。效果如下：

完整的源代码如下：

///////////////////////////////////////////////////
// 程序名称：视觉错觉艺术3
// 编译环境：Visual C++ 6.0 / 2010，EasyX_20210730
// 作　　者：yangw80 <yw80@qq.com>
// 最后修改：2014-7-14
//
#include <graphics.h>
#include <conio.h>


// 定义回调
void (*callback)(int x, int y);


// 圆中的每个点(回调函数)
void CirclePoints(int x, int y)
{
	if (x < y)
	{
		COLORREF c1 = getpixel(x, y);
		COLORREF c2 = getpixel(y, x);
		put

基于图形学中的 Bresenham 画圆法，设计了填充圆的实现。以下是该实现的 C 语言源码：

///////////////////////////////////////////////////
// 程序名称：基于 Bresenham 算法画填充圆
// 编译环境：Visual C++ 6.0 / 2013，EasyX 20140321(beta)
// 作　　者：yangw80 <yw80@qq.com>
// 最后修改：2014-7-14
//
#include <graphics.h>
#include <conio.h>

// 基于 Bresenham 算法画填充圆
void FillCircle_Bresenham(int x, int y, int r, COLORREF color)
{
	int tx = 0, ty = r, d = 3 - 2 * r, i;

	while( tx < ty)
	{
		// 画水平两点连线(<45度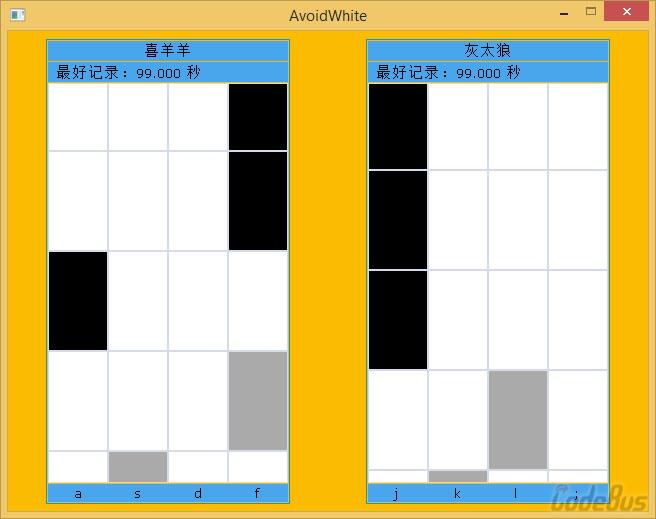

这就是当前十分流行的游戏“别踩白块儿”的双人版，两个人可以同时进行游戏。

默认情况下，喜羊羊的四个按键是 asdf，灰太狼的四个按键是 jkl;，可以在代码中修改。

以下是游戏截图：

以下是完整的游戏源代码，在 VC6.0 和 VC2013 下面测试通过。

///////////////////////////////////////////////////
// 程序名称：别踩白块儿（双人版） VC 源代码
// 编译环境：Visual C++ 6.0、2013，EasyX 20140321(beta)
// 作　　者：yangw80 <yw80@qq.com>
// 最后修改：2014-5-26
//
#undef UNICODE
#undef _UNICODE
#include <graphics.h>
#include <conio.h>
#include <stdio.h>
#include &

这是网上经常见的视觉错觉艺术图片，可以用程序生成的。效果如下：

完整的源代码如下：

///////////////////////////////////////////////////
// 程序名称：视觉错觉艺术2
// 编译环境：Visual C++ 6.0，EasyX 2013霜降版
// 作　　者：yangw80 <yw80@qq.com>
// 最后修改：2013-12-16
//
#include <graphics.h>
#include <conio.h>

// 定义常量
#define	UNIT		24
#define OFFSET_X	116
#define OFFSET_Y	36

// 画装饰花
void DrawUnit(int x, int y, int shape)
{
	// 设置颜色
	int n = ((shape & 1) ? 1 : 0) + ((shape & 2) ? 1 : 0)

这是网上经常见的视觉错觉艺术图片，可以用程序生成的。效果如下：

完整的源代码如下：

///////////////////////////////////////////////////
// 程序名称：视觉错觉艺术1
// 编译环境：Visual C++ 6.0，EasyX 2013霜降版
// 作　　者：yangw80 <yw80@qq.com>
// 最后修改：2013-12-16
//
#include <graphics.h>
#include <conio.h>

// 定义常量
#define	UNIT		15
#define OFFSET_X	122
#define OFFSET_Y	23

// 画每个小单元
void DrawUnit(int x, int y, int shape)
{
	// 定义颜色
	static COLORREF c[4] = {0x0000ff, 0x0077ff, 0x00ddff, 0x007

为什么要用配置文件

需要使用配置文件的场景很多，例如：

• 应用程序启动的时候，通过读取外部的一个“配置文件”，以加载不同的值，实现程序按照不同的需求来执行。
• 应用程序启动后，用户会有各种操作。当用户下一次启动应用程序时，就会希望保持上一次的操作状态。或者游戏结束后，需要将最高分记录等等。因此，可以在程序关闭的时候，将一些必要的变量保存下来，并且在下一次程序启动的时候，读取这些变量。通常，可以把这些变量保存在“配置文件”中。

创建配置文件

配置文件一般以 .ini 为扩展名，编码为 ANSI 或 Unicode（即 UTF-16 LE）。例如在 \windows 文件夹里面可以找到很多 .ini 文件。.ini 文件的内容是纯文本的，可以直接双击打开编辑。举一个实际例子，下面是一个标准的 .ini 配置文件的内容：

; EasyX 范例
[Ball]
x=10
y=37
r=20
[Wall]
width=

游戏说明：

矿井里的电路又出问题了。迅速借助你的头灯，在漆黑的矿井里找到出口逃出去吧。

控制说明：

• 方向键：移动
• A/S/D/W：移动
• 鼠标：控制照射方向
• F2：重来一局
• ESC：退出游戏

就不放抓图了，有兴趣的运行一下代码看看效果吧，【点这里下载编译后的 exe 文件】。

以下是全部源代码：

///////////////////////////////////////////////////
// 程序名称：矿井逃生
// 编译环境：Visual C++ 6.0 / 2010，EasyX_20200727
// 作　　者：yangw80 <yw80@qq.com>
// 最后修改：2013-11-15
//
#include <graphics.h>
#include <time.h>
#include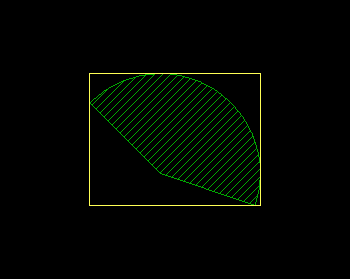 

今天很偶然需要这样一个东西：

求任意扇形的最小包围矩形，要求矩形的边是水平、垂直的。

这个东西看似很简单，但是仔细一想，需要注意的地方蛮多的，还真有点不好下手。再回想一下，好像没有那本书里面讲过。然后百度了一下，似乎也没找到有效的方法。于是我就花了点时间搞定了这个东西，然后顺手写了一个例子演示效果。

如果您有更好的方法，十分期待交流一下。

以下代码除了包含必要的求解任意扇形的最小包围函数之外，还加上了鼠标操作：按下左键移动鼠标，可以调整终止角的弧度；同时按下 Shift 键移动，可以调整起始角的弧度。

执行效果如图：

完整代码如下：

///////////////////////////////////////////////////
// 程序名称：计算扇形的最小包围矩形
// 编译环境：Visual C++ 6.0 / 2019，EasyX 20210730
// 作　　者：yangw80 <yw80

今天是 2013 年光棍节，写个程序庆祝一下，呵呵。

本程序模拟了这样一个场景：一个空地上乱七八糟地堆了一些货物，一个孤独的仓库管理员，带了一盏油灯，去巡视这些货物。

在鼠标的位置会亮起一盏油灯，随着鼠标的移动，部分光线会被仓库的货物遮挡。

就不抓图了，有兴趣的运行一下代码看看效果吧，【点这里下载编译后的 exe 文件】。

以下是全部源代码：

/////////////////////////////////////////////////////////
// 程序名称：带一盏油灯去巡视仓库
// 编译环境：Visual C++ 6.0 / 2010，EasyX 2013霜降版
// 作    者：yangw80 <http://hi.baidu.com/yangw80>
// 最后修改：2013-11-11
//
#include <graphics.h>
#include <conio.h>
#include &

由于某些学校的硬性规定，课设必须用 Borland C++ 3.1(以下简称 BC) 一类 DOS 下的编程工具完成。

但是，BC 用起来很费劲，毕竟是 dos 时代的工具，无论编辑还是调试，都很吃力。尤其是图形程序，由于涉及到硬件及系统的问题，导致程序不能在 win7 及以上版本的 Windows 中运行，必须借助 dosbox 一类工具或者虚拟机才可以，麻烦多多。

本文通过一些常用的技巧，讲解怎样用 Visual C++(以下简称 VC) 编写可以在 BC 下直接编译运行的程序。

这样做的好处就是，可以节约大量的编码和调试时间。众所周知，当程序规模比较大的时候，调试时间会超过编码时间。而 VC 的强大调试功能，远不是 BC 能比的。同时，windows 下便捷的编辑环境，也比 BC 能节约很多时间。再比如有些人的显示器可以旋转，将 24 寸的显示器旋转 90 度竖着用，一屏可以阅读上百行代码，这种效率，绝对不是 BC 那一屏 20 多行代码可以比的。即便 BC 启用 43 行模式，效果仍然很差。

所以，下面的这个方法看似

本文适用读者：已经学完 C 语言基本知识，并对 EasyX 略有了解。

本文范例实现的功能：文字在背景上移动，并且不破坏背景。

本文范例编译平台：VC6 / VC2010 + EasyX 20140321(beta)。

本文并不直接写出最终代码，而是从最开始绘制背景，一步步拓展到我们需要的功能。希望这个过程能对初学者有所启发。

一、绘制背景

为了实现文字移动而不破坏背景的效果，我们先画个背景。做法很简单，就是画一连串的竖线，并且每次变换颜色，这样就能弄一个渐变色的背景，代码如下：

#include <graphics.h>
#include <conio.h>

// 主函数
void main()
{
	// 创建绘图窗口
	initgraph(640, 480);
	
	// 绘制背景
	for(int i = 0; i < 640; i++)
	{
		setlinecolor(i);
		line(i,

又是一个怀旧的游戏，让我想起了以前学习编程的时候。

这个游戏模仿的微软在 20 多年前的一个小游戏，不知道谁也有印象呢？图片都是从原来的游戏中抓图弄出来的，颜色也是从原游戏抓图中取色设置的，应该和原来的风格很像。

你的任务是用香蕉击中你的对手。

你可以通过鼠标调整投掷香蕉的角度和力度，香蕉会受重力加速度的影响。同时，请注意屏幕底部表示风力的箭头，香蕉同样会受风力影响。风力的箭头越长，表示风力越强。还有，周围的楼宇会阻挡你的香蕉。

游戏运行效果如下：

完整的源代码和图片可以【点击这里下载】。

也可以直接查看如下游戏源代码（注意，除了以下代码，还需要两个图片文件，在前面的压缩包里面有）：

// 程序名称：扔香蕉的大猩猩
// 编译环境：Visual C++ 6.0 ~ 2019，EasyX_20210730
// 作　　者：慢羊羊 <yw80@qq.com>
// 发布日期：2012-9-23
// 最